HİPERBOLİK SAYILAR
Hiperbolik sayılar,Gerçel sayılarda olmayan ve karesi 1 olan bir sayının kümeye katılmasıyla üretilen kümeye hiperbolik sayılar kümesi denir. Tıpkı karmaşık sayılarda olduğu gibi, hiperbolik sayılar 
şeklinde yazılabilen sayılardır, ancak karmaşık sayılardan tek farkı hiperbolik birim denilen sayının
olarak tanımlanmasıdır. Bu sayılar fizikte, özellikle Özel görelilikte sıkça kullanılmaktadır.
Resmî tanım
polinom halkasında,
X2 − 1 polinomunun kökleri 1 ve -1 iken, bunların dışında başka bir 
sayısının da bu polinomun bir kökü olduğunun varsayılmasıyla oluşan
bölüm halkasına hiperbolik sayılar kümesi denir ve genelde 
ya da H ile gösterilir.
Böyle bir sayının polinom halkasının katsayılar kümesi olan gerçel sayılar kümesi 
'de de olmadığı görülebilir (ya da bu sayı yine 1 ya da -1 sayılardan birine eşit olmak zorunda kalır). Böylece bu sayı kümesi cebirin temel teoremi gereği bir cisim olamaz, değişmeli bir halka olur.
KARMAŞIK SAYILAR
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. Karmaşık sayılar şu biçimde gösterilirler
Genel olarak karmaşık sayılar için "z" harfi kullanılır. a ve b sayıları gerçel olup 
özelliğini sağlayan sanal birime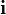 
denir. Kimi zaman özellikle elektrik mühendisliğinde 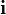yerine, 
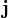kullanılır.
Ayrıca matematikte bu sayıların uzayı 
olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizce'de karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen kompleks sözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.
Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Diğer bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar.
Bir z karmaşık sayısının gerçel ve sanal parçaları sırasıyla Re(z) ve Im(z) şeklinde gösterilir. Bütün bu tanımları ve özellikleri bir örnekte gösterelim.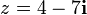 
uzayında bir karmaşık sayıdır. Gerçel sayılar, karmaşık sayıların alt kümesi olduğu için, uzayındaki cebrin hepsi dolayısıyla uzayında da tanımlıdır. Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.
Tanım
Karmaşık sayılar kümesi birçok şekilde tanımlanabilir. Aşağıdaki tanımların hepsi birbirine eşyapısaldır, yani yapısal olarak biri diğerinin yerine kullanılabilir. Bu yüzden aslında içerik olarak farklı olan aşağıda tanımlanan tüm kümeleri aynı harfle gösterdik, . Ayrıca bu simge, sadece karmaşık sayılar dediğimiz öğeleri içeren bir küme olmaktan ötedir, üzerine tanımlayacağımız iki tane ikili işlemi olan bir cisimdir. Üstelik bu cisim, gerçel sayıların en büyük cisim genişlemesidir, yani gerçel sayıları bundan daha fazla genişletemeyiz. Gerçel sayılarla karmaşık sayıların aynı kardinaliteye (öğe sayısına) sahip olduğunu da unutmayalım.
Kartezyen uzay tanımı
Gerçel sayılar kümesinde her sayıyı 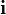ile çarparsak elde ettiğimiz 
kümesi önceki
olarak tanımlanmış olur. Bu 2 boyutlu kartezyen uzay, Argand düzlemi olarak anılır. Eğer yerine tamsayılar cismi 
alınırsa oluşan karmaşık tamsayılar Gauss düzlemindedir. Bu sayılara da Gauss sayıları denir.
Karmaşık sayılar, bu tanımla aşağıdaki gibi ifade edilir: 
olmak üzere;
z = (a,b)
Burada açıkça Re(z) = a ve Im(z) = b dir.
Cisim genişlemesi tanımı
Karmaşık sayılar, gerçel sayılar cisminin bir cisim genişlemesidir. 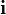sayısı x2 + 1polinomunun köklerinden biridir ve diğer kökü de 
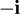olur. Bu iki öğenin gerçel sayılarla olan genişlemesinin eşyapısal olduğu kolaylıkla görülebilir:
Bu durumda
olarak tanımlanır. Daha açık olarak, karmaşık sayılar gerçel sayılar polinom halkasının x2 + 1 polinomuyla üretilen bölüm halkasıdır:
Bu bölüm halkasında X öğesinin görüntüsü 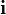karmaşık birimidir. Bu sayede karmaşık sayılar halkası cebirsel olarak kapalı olur ki bu, gerçel sayıların cebirsel kapanışıdır. Cebirin temel teoremi bunu gerektirir, n dereceli her polinomun tam n kökü vardır. Biz, her karmaşık sayının 
olarak ifade edildiği bu tanıma daha âşinâyız.
Matris (dizey) tanımı
Karmaşık sayıları, gerçel katsayılı 2x2'lik matrislerin bir altkümesi olarak düşünebiliriz. Birim sayıları
ve 
olarak tanımlanırsa böylece her bir karmaşık sayı
olarak ifade edilebilir ki burada a,b 
alınmıştır. Kaldı ki
olduğu kolaylıkla görülebilir. O halde karmaşık sayılar
şeklinde tanımlanmış olur.
Karmaşık sayılarda işlem
Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir. Öncelikle iki karmaşık sayının eşitliğini verelim.
Eşitlik
Bir 
ve 
karmaşık sayıları için
z = w ancak a = c ve b = d iken geçerlidir.
Toplama
Bir ve karmaşık sayıları için
Çarpma
Bir ve karmaşık sayıları için
Eşlenik
Bir karmaşık sayısı için eşlenik ifadesi 
dönüşümüdür ve
ya da matrislerde
olarak tanımlanır.
Eşleniğin cebirsel özellikleri sayısı gerçel kısmı Re(z) = 4, sanal kısmı Im(z) = − 7 olan kümesine eşyapısaldır. Karmaşık sayılar cismi ise buradan hareketle
ancak z gerçel sayı olduğunda geçerlidir.
Bir karmaşık sayı ile eşleniğinin karmaşık uzaydaki gösterimi.
Mutlak Değer
Bir karmaşık sayısı için
ya da
olarak tanımlıdır.
Mutlak değerin cebirsel özellikleri
ancak 
iken geçerlidir.
(üçgen eşitsizliği)
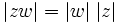
Çarpımsal Ters
Bir karmaşık sayısının tersi
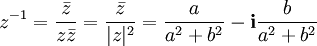
olarak ya da bir matrisin tersine uygun olarak
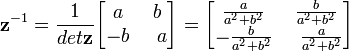
olduğu görülür.
Bölme
Bir ve karmaşık sayıları için
Çifte Karmaşık Sayılar
İki tane karmaşık birimi olan ya da bir tane hiperbolik iki tane de karmaşık birimi olan kümeye çifte karmaşık sayılar kümesi denir. Bu kümede her sayı
şeklinde ifade edilebilir. Ancak dörtlük sayılarla karıştırılmamalıdır. Çünkü bu kümede
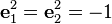
iken
olarak tanımlanır. Zira, bu sayılar dörtlük sayıların değişmelisi olarak anılır.
Bu maddede çifte karmaşık sayı,
olarak gösterilecektir.
Tanım
Çifte karmaşık sayılar birkaç şekilde tanımlanabilir. En yaygın tanımı iki farklı karmaşık sayı kümesinin birleştirimi olduğu için küme çifte karmaşık sıfatını almıştır.
İki karmaşık birim sayı tanımı
İki farklı karmaşık sayı kümesi olduğunu varsayalım: 
ve 
. Her birinin karmaşık birimleri sırasıyla 
ve 
olsun. Bu durumda bu iki birimin çarpımı
olarak tanımlanır ve bu sayıya 'hiperbolik birim sayı adı verilir. Açık olarak görülür ki bu birim sayı,
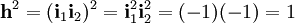
özelliğini sağlar. O halde bir çifte karmaşık sayı
olarak ifade edilebilir.
Karmaşık katsayılı hiperbolik sayı tanımı
Eğer hiperbolik sayı tanımını
gibi karmaşık katsayılı olarak alırsak her çifte karmaşık sayı
şeklinde ifade edilecektir. Burada
olarak tanımlamakla her çifte karmaşık sayıyı
şeklinde ifade etmiş ve istediğimiz özellikleri sağlamış oluruz.
AŞKIN SAYI
Matematikte cebirsel olmayan herhangi bir reel sayıya aşkın sayı denir. Diğer bir deyişle, katsayıları tamsayı (ya da rasyonel) olan bir polinomun kökü olamayan reel sayılara aşkın sayı denir. Buradan, tüm aşkın sayıların irrasyonel olduğu sonucuna varılabilir. Ancak tüm irrasyonel sayılar aşkın sayı değildir, örneğin √2 irrasyoneldir, ancak x2 − 2 = 0 polinomunun bir köküdür.
Aşağıdaki sayılar, aşkın olarak bilinir:
